Lyapunov equation plays a prominent role in model reduction methods, such as balanced truncation and frequency cut of approximation. In practical implementations for large dimensional systems, low rank approximations are usually computed. The fundamental issue involved is the accuracy of such approximations, which requires analysis of the decay rates of eigenvalues of the solution to the Lyapunov equation. The issue is also relevant for linear autonomous control systems, whose observability and controllability Gramian are solutions to two Lyapunov equations, as well as for algebraic Riccati equations. The singular values of the solution to the latter equation can be related to the singular values of a Gramian.
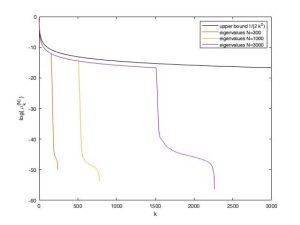
The existing results, assuming appropriate regularity, boundedness and finite rank assumptions of the operators involved, show that singular values of the solution to the Lyapunov equation decay (at least) exponentially in the square root, i.e. of order O(exp(-√k)) [GK14, O15]. Generalisation of the results from algebraic equations to the differential case was done in [S18]. These works consider the upper bounds only, while we aim to identify both lower and upper ones, as well as to analyse their optimality, paying a special attention to control systems. The preliminary investigations in this direction suggest that the set of eigenvalues consists of two subsequences that do not exhibit the same decay property (Figure 2). This would imply that the lower bounds follow a different law than the upper ones. Verifying this conjecture and explaining the gap between the bounds is a significant challenge that we will address in this work package. In addition, we want to establish a more precise connection between the bounds and the spectrum of the operator generating the dynamics. In particular, we want to express the estimates explicitly in terms of eigenvalues of the latter operator, which has not been presented in the scientific literature so far. The transformation of the decay bounds when the system dynamics changes and loses some of its properties (such as control, observability, etc.) will be of special interest.
The topic will be also considered in the framework of parameter dependent problems, where one wants to avoid solving the same type of equation (e.g. the Lyapunov one) from scratch for each new parameter value. Model order reductions play a prominent role here, and, as already pointed out, a rapid eigenvalue decay is crucial for efficient approximation of problems by lower dimensional ones. Previous results in that direction were obtained in [SS17, LW21] for algebraic Lyapunov equations by the use of reduced model 2 Application Form Conduction techniques (POD, greedy algorithms). Here we plan to generalise results to differential Lyapunov equations, as well as to Riccati ones. In addition, we aim to implement machine learning techniques which will improve the efficiency of the online phase of the algorithm.
Literature:
- [GK14] Grubišić, L; Kressner, D: On the eigenvalue decay of solutions to operator Lyapunov equations. Systems & Control Letters, 73, 42-47 (2014)
- [LW21] Lazar, M; Weston, J: Greedy Algorithm for Parameter Dependent Operator Lyapunov Equations. Systems Control Letters, 154, 104968 (2021)
- [O15] Opmeer, M. R: Decay of singular values of the Gramians of infinite-dimensional systems. 2015 European Control Conference (ECC), 1183-1188 (2015)
- [SS17] Son, N; Stykel, T: Solving parameter-dependent Lyapunov equations using the reduced basis method with application to parametric model order reduction, SIAM J. Matrix Anal. Appl. 38(2) 478–504,
- [S18] Stillfjord, T: Singular Value Decay of Operator-Valued Differential Lyapunov and Riccati Equations, SIAM Journal on Control and Optimization, 56(5), 3598-3618 (2018)
