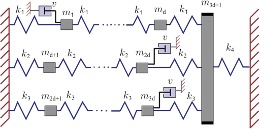
One of the crucial problems when attempting to control vibrational systems is the placement of dampers and it is still open in different disciplines (mathematics, engineering, physics, etc.). The problem arises from the consideration of the wave-like equations (see [BGTQRSS20] and references therein), where after an appropriate discretization we consider the dynamics of the second order system of ordinary differential equations (ODEs). Thus, the main problem we try to solve will be that for a given vibrational system (for example like (3n + 1)-mass oscillator on Figure 4) determine the “best damping” (meaning the type and the dampers’ positions) which ensures some optimality in the solution of the corresponding system of ODEs, independent of initial data, like initial position and velocity. The possible (different) structures of the damping can be found in [GR14] or [A14]. For example, in civil engineering, the design of supplemental dampers in multistory structures has been considered in [GGRL96]. An overview of different methods for the optimal design of passive dampers in civil engineering is given in [T09]. Another example from hydraulic engineering is the (additional) damping of vibration compensators for hydraulic systems [MR03]. Whereas the latter example for the special case of the undamped Mikota vibration compensator was thoroughly 3 Application Form Conduction investigated e.g. in [WMA18], an in-depth investigation of the optimal damping is still missing. However, the first investigations are documented in [WZ18]. Based on recent theoretical results on controllability and stability of second-order infinite dimensional systems coming from elasticity [AN15], we plan to prove theoretical results on the best positions for a damper of rank one with respect to both criteria (total average energy and minimal displacement) for a string and a beam free vibrations. The crucial difference in our approach from [JAAD22], [HH03] or [CZ94], consists in different assumptions on damping and optimization criteria. Also we plan to develop an approach for the dampers’ optimization for a general mechanical system, with the external damping of the rank two or more. Thus, the main focus of our investigation will be solving the problem of optimal positioning of dampers in vibrational systems with different structures, like the vibrational systems with internal damping and one without it or with numerically negligible internal damping.
Literature:
[A14] Adhikari, S.; Structural Dynamic Analysis with Generalized Damping Models: Identification. John Wiley & Sons, 2014 DOI:10.1002/9781118862971 [GR14] Geradin, M; Rixen, D. J.; Mechanical Vibrations: Theory and Application to Structural Dynamics, John Wiley & Sons, 2014. [GGRL96] Gluck, J; Gluck, N; Reinhorn, A M; Levy, R: Design of supplemental dampers for control of structures. Journal of Structural Engineering, ASCE, 122(12), pp. 1394–1399 (1996) [T09] Takewaki, I: Building Control with Passive Dampers: Optimal Performance-based Design for Earthquakes. John Wiley and Sons Ltd, (2009) [MR03] Mikota, J; Reiter, H: Development of a compact and tuneable vibration compensator for hydraulic systems. International Journal of Fluid Power, 4(1), pp. 17–30 (2003) [WMA18] Weber, W. E.; Muller, P. C.; Anders,B: The remarkable structure of the mode shapes and eigenforces of a special multibody oscillator, Archive of Applied Mechanics, 88(4), pp. 563–571(2018) [WZ18] Weber, W. E.; Zastrau, B. W: Model order reduction of mikota’s vibration chain including damping effects by means of proper orthogonal decomposition, Journal of Theoretical and Applied Mechanics, 56(2), pp. 511–521,(2018) [AN15] Ammari, K.; Nicaise,S.: Stabilization of Elastic Systems by Collocated Feedback , Lecture Notes in Mathematics, 2124, Springer, Cham, 2015. [JAAD22] Jouberta, A.; Allaire, G.; Amstutz, S.; Diani, J.; Damping optimization of viscoelastic cantilever beams and plates under free vibration, Computers & Structures, 268, (2022) [HH03] Hebrard, P; Henrot, A: Optimal shape and position of the actuators for the stabilization of a string, Systems & Control Letters, 48 pp. 199–209 (2003) [CZ94] Cox, S; Zuazua, E: The rate at which energy decays in a damped string, Comm. Partial Differential Equations, 19 pp. 213–243 (1994)
